
Cost Analysis of Current Design
By analysing the rate of heat flow in each individual stream we can find the stream that is contributing the most to the current cost. Our team discovered that stream 3 has an extremely high amount of heat energy wasted as it is cooled from 107 °C to a temperature of 40 °C. The cost associated with this is approximately £105,800.
01
Stream
Rate of heat flow
517 KJ/S
Cost per year
£29,780
02
stream
Rate of heat flow
545 KJ/S
cost per year
£21,370
03
stream
Rate of heat flow
2700 KJ/S
Cost per year
£105,800
04
stream
Rate of heat flow
130 KJ/S
cost per year
£7,480
05
stream
Rate of heat flow
1181 KJ/S
cost per year
£68,000
06
stream
Rate of heat flow
240 KJ/S
cost per year
£13,800
Problem Involving Stream 1 and 2
From the plant diagram (figure 1.3) we noticed that stream 1 and 2 were in close proximity to each other and had the capacity for heat exchange. This lead to our decision to implement a heat exchanger between streams 1 and 2. However, this is not enough to completely cool down stream 2 so we decided to add in an additional cooler to bring the temperature of the stream down to 40 degrees. Since our feed stream of cooling water is not effective at cooling streams under 60 degrees, we decided to add the cooler to stream 2 before the heat exchanger to make up for any lack of cooling done by the heat exchanger. All heat exchangers in our solution will be utilising counter current flow as it is able to extract a high proportion of heat energy from the hot streams than co-current over a smaller area which is cheaper.
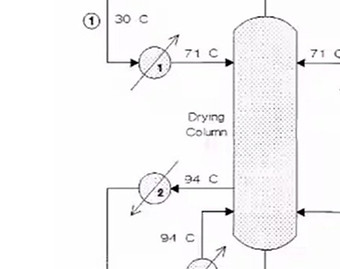
Figure 1.3

Figure 1.4
After implementing a heat exchanger between streams 1 and 2, the total cost over a period of 5 years is significantly lower at only 9% of the original cost of operation (£255,750 for streams 1 and 2). The cost per annum was calculated by adding the total running cost of the cooler over a period of 5 years, which costs £1,160 annually, with the cost of installing a heat exchanger divided by the total amount of running years.
*Calculated using a annual cooler running cost of £1,160.
Problem Involving Stream 3
The difficult task now falls on deciding which system of heat exchangers would provide the most optimum cooling of stream 3. We investigated 3 different ways of arranging heat exchangers along stream 3 to see which would bring about the cheapest and most effective option. In the end, this system of heat exchangers (figure 1.5) proved to be the most effective. By utilising the massive amount of heat energy in stream 3, we can use this to heat up streams 4,6 and 5. Note that the order of these streams must be in this order as the temperature of stream 3 coming out of each heat exchanger must be higher than the temperature of the cooler streams out of the next heat exchanger.
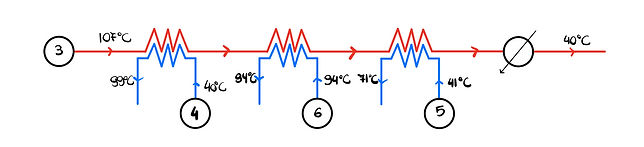.png)
Figure 1.5
Notably, stream 6 does does not have a change in temperature as all the energy is given to stream 6 in order to change states. Stream 4 and 5 do not experience a change of state.
Stream 3 & 4
No change of phase
T-in(hot)/°C
T-out(hot)/°C
T-in(cold)/°C
T-out(cold)/°C
Log mean temp
Area of heat exchanger/M^2
Cost
107
104
40
99
26.93
5.60
Stream 3 & 5
No change in phase
T-in(hot)/°C
T-out(hot)/°C
T-in(cold)/°C
T-out(cold)/°C
Log mean temp
Area of heat exchanger/M^2
Cost
98
69
40
71
27.99
4.90
Stream 3 & 6
Change of phase
T-in(hot)/°C
T-out(hot)/°C
T-in(cold)/°C
T-out(cold)/°C
Log mean temp
Area of heat exchanger/M^2
Cost
104
98
94
94
6.54
42.62
The total cost of installing this system of heat exchangers would be £29,819. The running cost of the cooler per annum would be £45,793.
When we combine our solution for streams 1 and 2 as well as the system of heat exchangers for stream 3 we find that the total cost over a period of 5 years is approximately £282,489. If we compare the running cost over 5 years of our solution to the running cost of the current design we find that our solution is almost one fifth of the current cost, a decrease of 77% in running cost. This is why we choose these set of solutions as the most optimum solution to the task given by the Imperial Chemical Company.
You can find a complete presentation explaining how and why we came to our conclusion in the video below. If you have any further questions please send them to icldesignteam1@gmail.com